Bases de l'électronique

Bon alors on va commencer par vraiment du très très simple avant de progressivement augmenter en difficulté (quand j'aurais la motivation de rédiger les prochains). Je ne vais pas prendre énormément de temps pour expliquer ce qu'est l'intensité, la tension et la résistance mais on peut les visualiser simplement de cette manière: Imaginez un tuyau dans lequel de l'eau circule. La tension c'est la pression de cette eau, l'intensité c'est son débit et la résistance c'est le diamètre du tuyau. Plus le tuyau est fin, plus la résistance est élevée. L'unité de tension est le volt (V), d'intensité est l'ampère (A) et de résistance l'ohm (Ω).
Prenons le circuit suivant:

Ici, le courant part de la "flèche" (symbole de l'entrée) et va vers la masse (en bas à droite). Il y a deux résistances dans le circuit. Comme elles sont en série ("branchées" l'une après l'autre), ils suffit d'additionner leur valeur. Le circuit a donc une résistance de:

R_{T} = R_{1} + R_{2}

R_{T} = 10 + 100 = 110 Ω

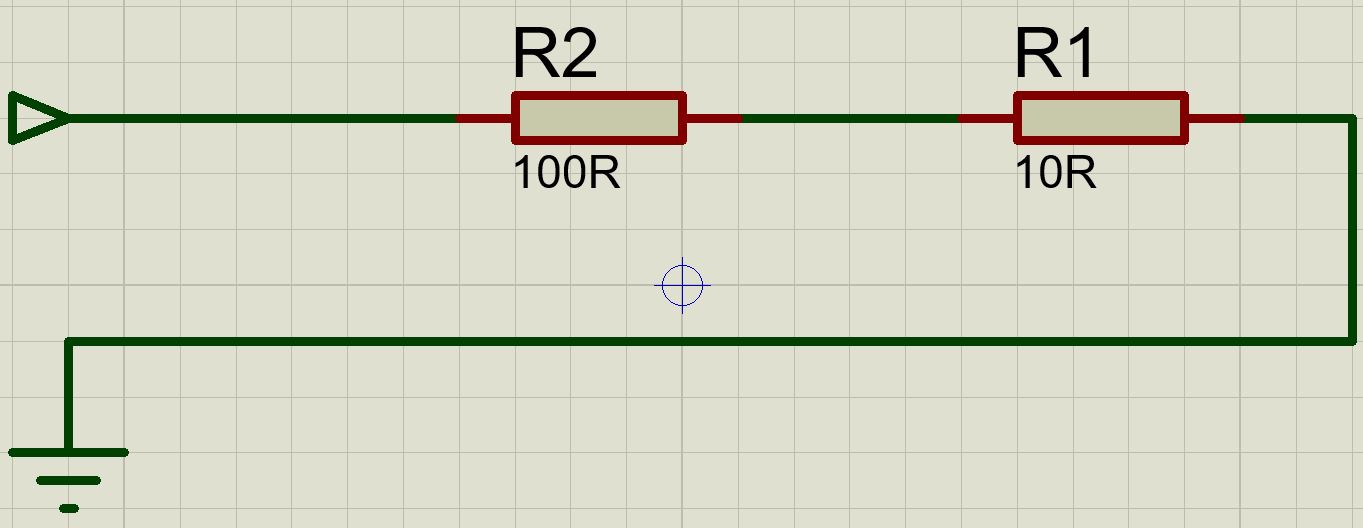
Rappellons-nous de la loi d'ohm:

U = R \cdot I

Avec U la tension, R la résistance et I l'intensité. Appliquons un courant au circuit d'une tension de 10V. On a alors:

10 = 110 \cdot I

On peut donc calculer l'intensité du courant qui traverse le circuit:

I = \frac{U}{R}

I = \frac{10}{110}

I ≅ 0.09 A

Ainsi, on sait que l'intensité du courant est de 90mA environ. Or, dans un circuit en série, l'intensité est la même en tout point du circuit, ce qui n'est pas le cas de la tension. Il nous est alors possible de calculer la différence de potentiel (la tension) aux bornes de chaque résistance. Calculons la tension aux bornes de la résistance 2:

U_{2} = R_{2} \cdot I

U_{2} = 100 \cdot 0.09

U_{2} = 9 V

Dans les calculs précédents, nous avons arrondi, la tenstion est donc d'environ 9V. Essayons sur l'autre résistance:

U_{1} = R_{1} \cdot I

U_{1} = 10 \cdot 0.09

U_{1} = 0.9 V

On peut alors additionner les tensions aux bornes des deux résistances:

U = U_{1} + U_{2}

U = 0.9 + 9

U = 9.9 V

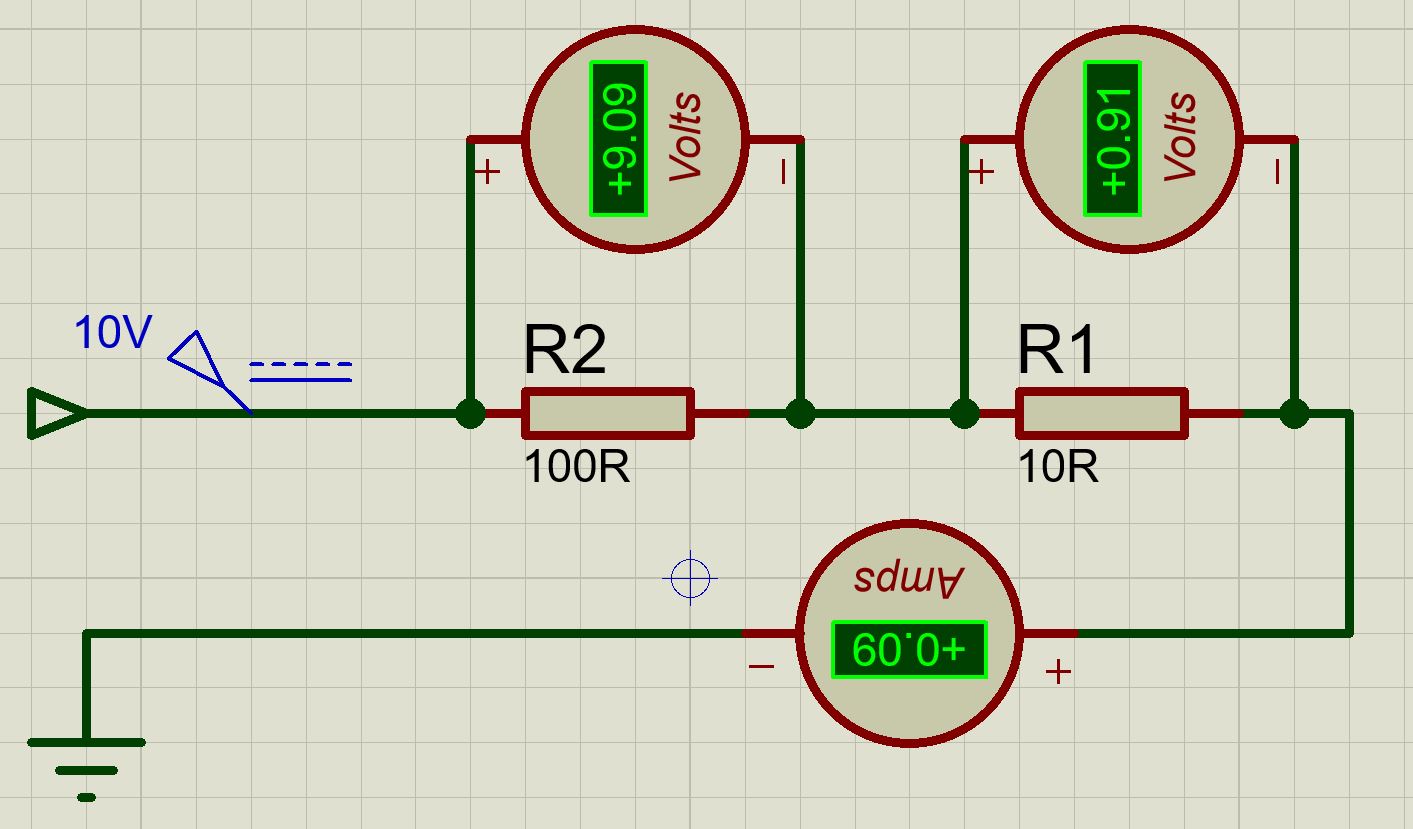
Nos calculs étant arrondis, on ne trouve que 9.9V, mais c'est très proche de la vraie tension qui passe dans le circuit, qui je le rappelle est de 10V. Représentation:

Cependant, dans un circuit en parallèle, les choses ne se passent pas de la même manière. La tension est la même en tout point du circuit mais pas l'intensité. Représentation de notre circuit en parallèle:

Ici, pour calculer la résistance totale du circuit, nous devons introduire la conductance: l'inverse de la résitance. Et c'est bien connu que pour inverser un nombre en mathématiques, il faut diviser 1 par ce nombre. On a alors:

G = \frac{1}{R}

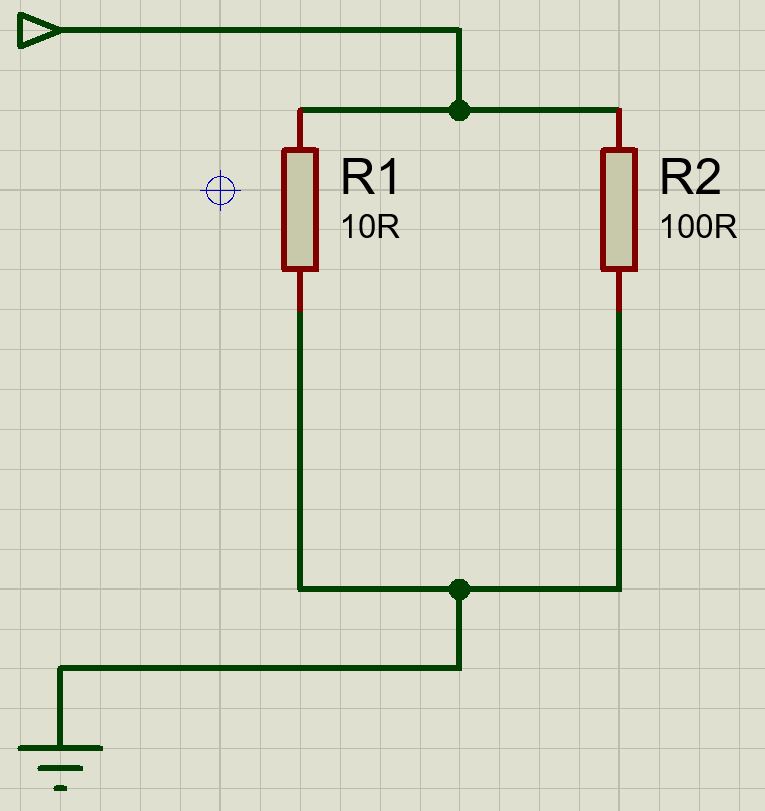
Cette inductance s'exprime en siemens (S). Pour calculer la résistance totale du circuit, nous devons d'abord additionner les conductances des résistances. Nous obtiendrons alors la conductance du circuit. Si on l'inverse, on obtient la résistance du circuit. Calculons la conductance totale:

G_{T} = G_{1} + G_{2}

G_{T} = \frac{1}{R_{1}} + \frac{1}{R_{2}}

G_{T} = \frac{1}{10} + \frac{1}{100}

G_{T} = \frac{11}{100} = 0.11 S

Calculons alors la résistance totale du circuit:

R = \frac{1}{G}

R = \frac{1}{0.11} ≅ 9.1 Ω

Le circuit a donc une résistance de 9.1Ω environ. Maintenant, calculons l'intensité du courant passant par chaque résistance:

U = R_{1} \cdot I_{1}

10 = 10 \cdot I_{1}

I_{1} = \frac{10}{10} = 1 A

U = R_{2} \cdot I_{2}

10 = 100 \cdot I_{2}

I_{2} = \frac{10}{100} = 0.1 A

Nous pouvons donc calculer l'intensité du courant passant dans tout le circuit:

I_{T} = I_{1} + I_{2}

I_{T} = 1 + 0.1 = 1.1 A

L'intensité du courant passant dans le circuit est de 1.1A. Représentation:

Nous pouvons donc vérifier avec la loi d'ohm que nos résultats sont corrects:

U = R \cdot I

9.1 \cdot 1.1 = U

9.1 \cdot 1.1 = 10.01 V

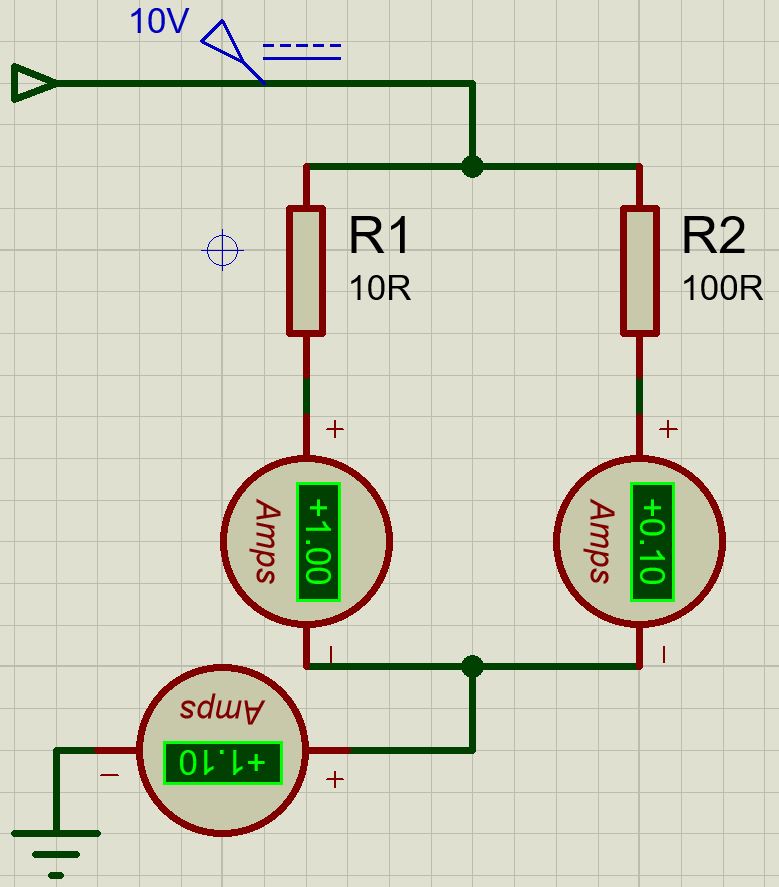
L'inexactitude de notre résultats est toujours dûe à nos approximations, mais on voit bien que tout correspond, on retrouve notre tension qui passe dans le circuit.