Sceeker's stuff

BONJOUr, CHANTIER EN COURS PARTEZ SVP

j'en ai marre parce que plus j'avanCE PLUS ON DIRAIT QUE CA VEUT RIEN DIRE BORDEL DE MERDE JE SAIS PAS VULGARISER ET EN PLUS A LA FIN MES RESULTATS sont NIQU2S DONC VOILA LA PAGE EST EN PAUSE VROOM VROOM CHANTIER DEGAGé svp
mdrrrrrrrr :)

h


meuglement de chat

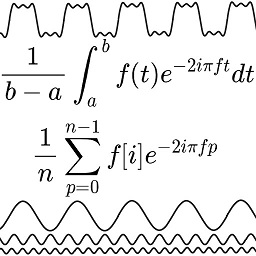
Note: Je vais tenter d'expliquer toutes les notions à partir de quasiment zéro pour qu'elles soient facilement accessible. Cependant mes capacité de vulgarisation et le temps vous pouvez accorder à cet article étants limités, il est possible que certains passages aient été trop rapidement couverts. Si c'est le cas mais que le sujet vous intéresse vraiment, je vous recommende vivement de faire de plus amples recherches par vous mêmes, il y a beaucoup de ressources sur le sujet sur Internet.

---

I - Préambule (attention digressions)

Qu'est-ce qu'une transformation de Fourier ? Pour faire très simple, c'est un outil mathématique qui permet de décomposer n'importe quelle fonction en une somme de fonctions sinusoïdales. Par exemple, pour illustrer vous pouvez prendre l'image en haut de ce poste: le signal en haut de l'image est décomposé en signaux que vous pouvez voir en bas de l'image. Et si on les additionne, cela donne à nouveau le signal de base.
Au tout début, lorsque le mathématicien français Josh Fourier a découvert cela, il développa les séries de Fourier pour décomposer les fonctions périodiques. Mais il n'aura pas fallu longtemps avant que la transformation de Fourier, une extension des séries de Fourier qui permet d'appliquer ce principe sur les fonctions non périodiques, voit le jour.
Nous nous attaquerons à la définition plus mathématique (bien que toujours vulgarisée) après. En attendant, il faut savoir que tout cela ne s'applique qu'à des fonctions mathématiques continues, analogiques. Or, dans la vie de tous les jours, cela n'est pas très pratique. Imaginons que nous voudrions décomposer une note d'un instrument musical à partir d'un enregistrement. Il faudrait d'abord modéliser le signal de l'enregistrement en fonction mathématique, ce qui, avouons-le, serait très complexe. Il existe donc une autre extention de la transformation de Fourier pour les signaux discrets: la transformation de Fourier discrète.

Mais c'est quoi ces histoires de discrétion ? En mathématiques, on dit que quelque chose est discret lorsque sur un intervalle fini, il y a un nombre fini de valeurs. Par exemple, une suite est discrète, car elle ne s'incrémente que de un par un, alors qu'une fonction peut s'incrémenter par 0.1, 0.01, 0.001 etc sans limite.
Reprenons notre exemple d'un enregistrement d'un son. Pour comprendre pourquoi il s'agit d'un signal discret il faut s'attaquer au fonctionnement d'un microphone numérique. Et pour cela, il faut rappeler ce qu'est le son. Le son, c'est simplement des vibrations de l'air: celui-ci se compresse et se décompresse. Or, un microphone est composée d'une membrane qui va bouger selon les compressions/décompressions de l'air. Et cette membrane est attachée à un petit aimant autour duquel se situe une bobine électrique. En bougeant, les champs électromagnétiques de l'aimant vont, par induction, générer un champ électrique dans la bobine. Et ainsi, un ordinateur va capter ce courant électrique et l'interprêter. Un microphone ne mesure donc que l'amplitude du son: la pression plus ou moins forte effectuée par l'air sur sa membrane. Mais il est impossible pour un ordinateur d'enregistrer de manière continue l'amplitude du son. Il ne va donc l'enregistrer qu'une fois toutes les X secondes, où X est le taux d'échantillonnage: l'intervalle fixe entre chaque enregistrement d'amplitude. Le signal qui va donc résultat de cet enregistrement est discret ! Il n'y a des valeurs qu'à certains points du temps donnés et pas à une infinité de points.

Ainsi, dans la vie de tous les jours, que vous vous rendiez compte ou non, les transformations de Fourier discrètes sont très communes et importantes. Sans elles, il n'y aurait pas eu de traitement de signal qui aurait pu permettre l'électronique moderne. Mais il reste un problème. Vous comprendez plus tard qu'appliquer cette transformation directement peut être très demandante en calculs. Par exemple, pour un signal composé de ${10}^{18}$ points, cela pourrait prendre environ 32 ans de calculs. Ce n'est pas envisageable. Peu de temps après la publication des travaux de Fourier, un très grand mathématicien, Carl Friedrich Gauss, mis au point un algorithme permettant d'optimiser de manière folle le nombre de calculs à effectuer, réduisant grandement le temps d'application de la transformation discrète. Cependant, à son époque, comme cela lui sembla peu utile il ne publia jamais rien sur le sujet. Cependant, 160 ans plus tard, dans l'ère du numérique, Deux mathématiciens: Cooley et Tukey, ont redécouvert cet algorithme et l'ont popularisé. C'est aujourd'hui l'algorithme de DFT (transformation de Fourier discrète) le plus répandu et connu bien qu'il existe de nombreux algorithmes de FFT (transformation de Fourier rapide, comprenant tous les algorithmes de calcul de DFT) aujourd'hui.
Petit bonus: tous les algorithmes de FFT utilisent la notion de nombres complexes. Cependant, une sorte de transformation de Fourier un peu spéciale existe: la transformation d'Hartley. Et les algorithmes de calcul de la transformation d'Hartley discrète eux ne nécessitent pas de nombres complexes, ce qui semblerait donc permettre des temps de calculs plus rapides... Cependant la vérité est un peu plus complexe. Affaire à suivre?

II - Fonctionnement de la transformation de Fourier

Afin de comprendre et d'illustrer la transformation de Fourier, nous allons avoir besoin d'utiliser les nombres complexes comme nous l'avons expliqué précédemment. Pour ceux qui n'auraient encore jamais entendu parlé de cela, je vais essayer d'expliquer cela assez brièvement. Afin de pouvoir résoudre certaines équations qui n'étaient pas résolvables dans les ensembles numériques plus communs (nombres entiers, réels etc), les mathématiciens ont inventé un ensemble comportant un nombre un peu spécial, qui lorsque monté à la puissance deux (mis au carré), vaut -1. Ce nombre, noté i, ne dispose pas de valeur numérique réel: c'est un nombre imaginaire qui, au carré, vaut -1. De cet ensemble de nombre, nommé l'ensemble complexe $\mathrm{ℂ}$, découle donc une nouvelle quantité illimitée de nombres dits "complexes". Un nombre complexe se compose de deux parties: une partie réelle (composée d'un nombre appartenant à l'ensemble des réels $\mathrm{ℝ}$) et une partie imaginaire. La partie imaginaire s'écrit sous cette forme:
$y·i$
Où y est un nombre réel représentant la partie imaginaire et i l'unité imaginaire, le nombre dont nous avons parlé précedemment. Ainsi, un nombre complexe z s'écrit comme ceci:
$z=\alpha +y·i$
Avec x notre partie réelle. La notation pour la partie réelle ou imaginaire de z est la suivante:
$Re\left(z\right)=\alpha$
$Im\left(z\right)=y$
On peut donc se demander comment on représenter un tel nombre. Et bien pour cela on utilise un repère classique, mais dans lequel un seul nombre complexe correspond à un point avec deux coordonnées. Pour cela on décompose notre nombre: sa partie réelle sera son abscisse et sa partie imaginaire son ordonnée. Prenons par exemple le nombre complexe suivant:
$3+2i$
Pour les coordonnées d'un nombre complexe, on parle d'affixe. Ici, si on associe ce nombre à un point P, le point P aurait pour affixe:
$P\left(3;2\right)$
Cette façon que nous avons utilisé pour exprimer un nombre complexe s'apelle la forme algébrique. Mais il existe deux autres formes: la forme trigonométrique et la forme exponentielle. Cela n'étant pas le sujet ici, je vais juste vous dire que la forme exponentielle du complexe z s'écrit de la manière suivante:
$\lambda ·e^{i·\theta }$
Où e est le nombre d'Euler (un autre très grand mathématicien): une constante irrationnelle valant approximativement 2.7 et qui, lorsque montée à la puissance x, forme la fonction exponentielle connue pour croître très rapidement. Dans cette forme, on appelle $\lambda$ le module du nombre complexe: il correspond à la distance séparant son point de l'origine du repère. Et on nomme $\theta$ l'argument du nombre complexe, qui correspond à l'angle entre l'axe des abscisses et la droite entre l'origine et le point du nombre complexe. Voilà une illustration:
Ainsi, lorsque $\theta$ varie, le point tourne autour de l'origine (celui-ci s'exprimant en radians, $2\mathrm{\pi }$ correspond à un tour complet autour du cercle origine-point). Et lorsque $\lambda$ varie, le point s'éloigne plus ou moins de l'origine.
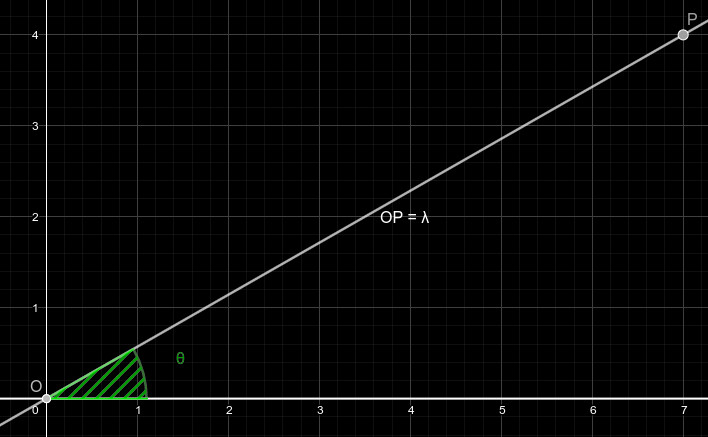
Pour tenter d'illuster cela, imaginons que $\theta$ ne cesse d'augmenter pendant que $\lambda$ oscille de cette manière, comme si on avait un enregistremnt audio d'un signal triangulaire pur:
Ainsi, dans notre forme exponentielle de tout à l'heure, cette l'oscillation discrète écarte plus ou moins le point de l'origine. Or, $\theta$ augmente de manière infinie, donc le point tourne autour de l'origine, à une distance $\lambda$ de l'origine. C'est en fait comme si on "enroulait" l'oscillation autour d'un cercle qui aurait pour centre l'origine:
C'est comme si au lieu de représenter notre signal sur un repère classique, on le faisait s'enrouler autour de l'origine sans jamais s'arrêter. Essayons de modifier notre forme exponentielle afin de l'exprimer en fonction du temps et de notre signal discret. On dit qu'un signal discret peut s'exprimer sous la forme d'un tableau de valeur. C'est à dire, par exemple, de cette manière:

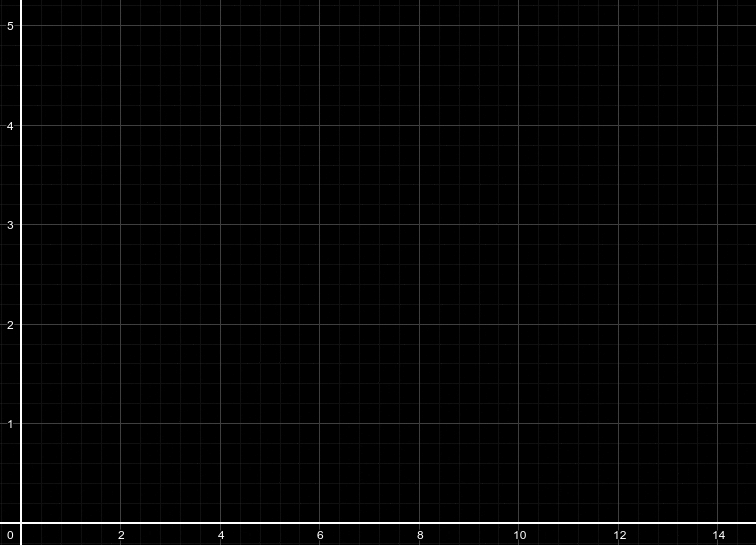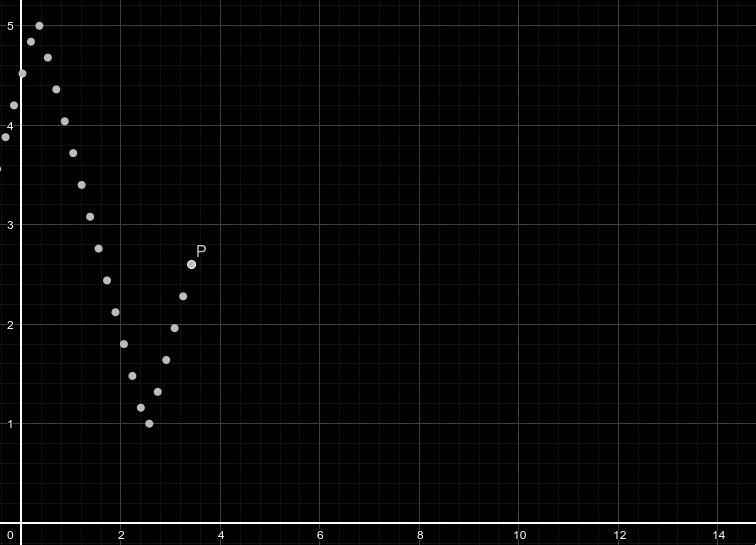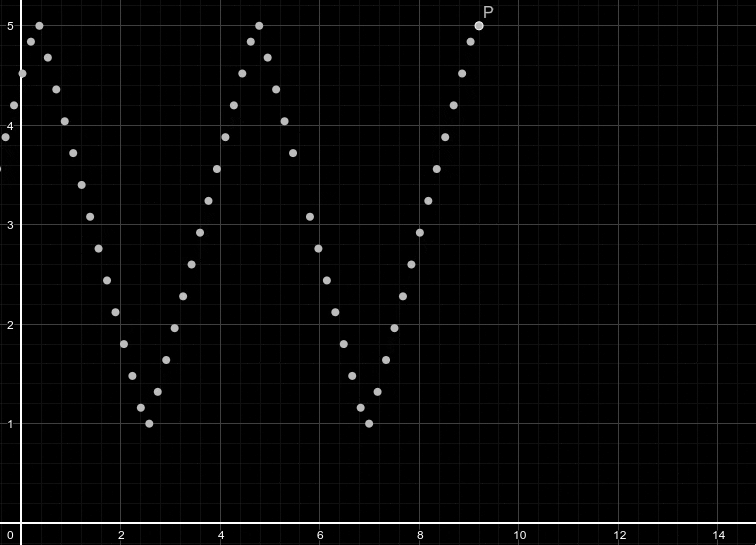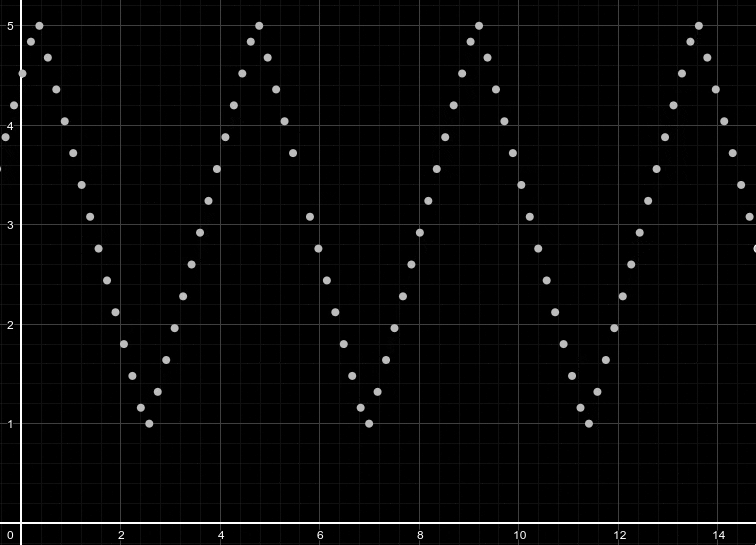
Temps t (s)	1	2	3	4	5	6	7	8	9	10	11
Amplitude	0	0.5	1	1.5	2	2.5	3	3.5	4	4.5	5

Ainsi, on introduit cette notation:
$\alpha \left[t\right]=\lambda$
Où $\alpha$ représente notre signal. Par exemple, selon notre tableau de valeur précédent, on a:
$\alpha \left[8\right]=3.5$
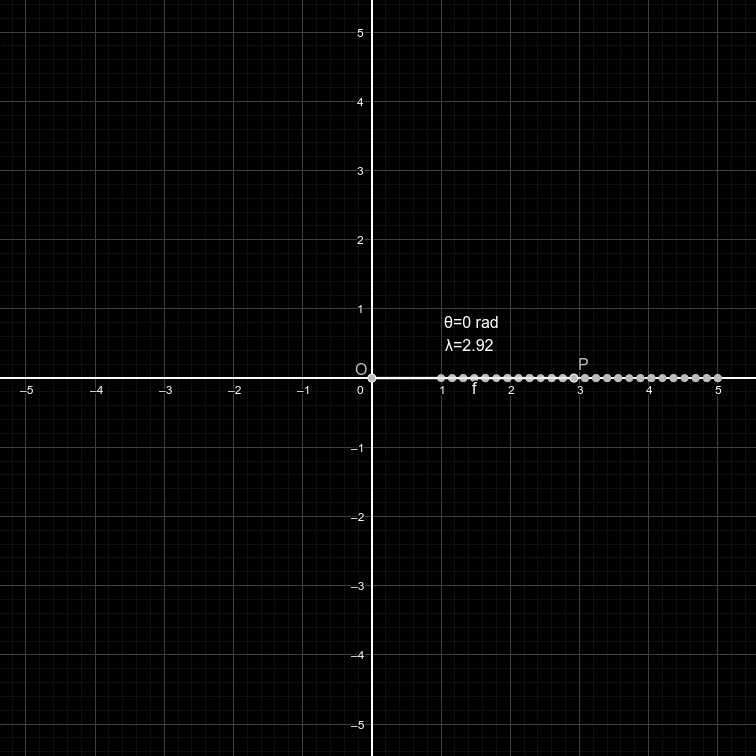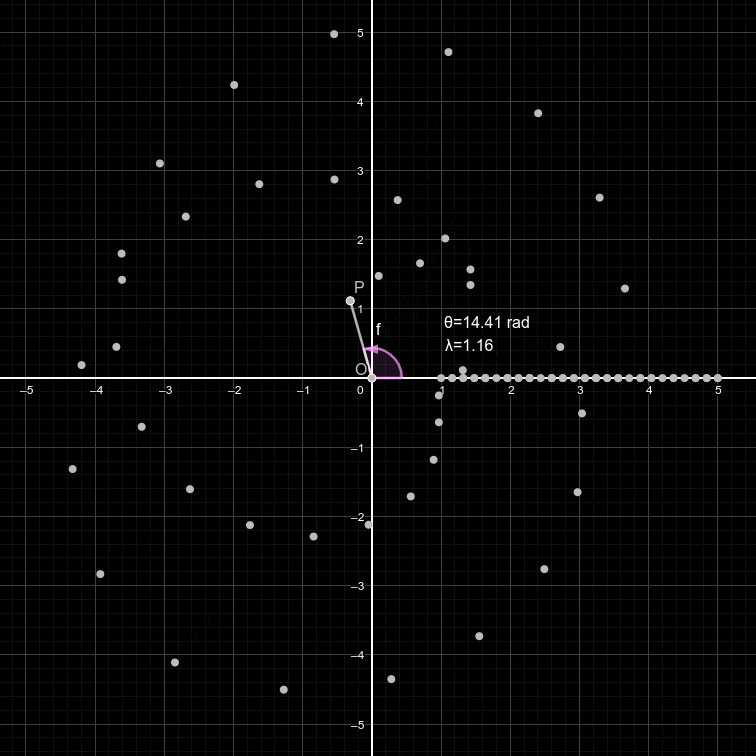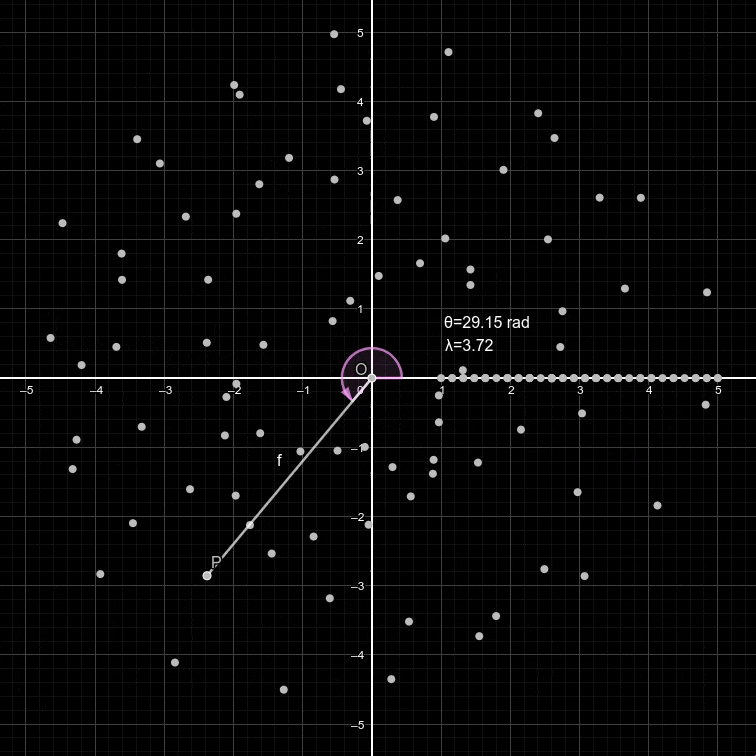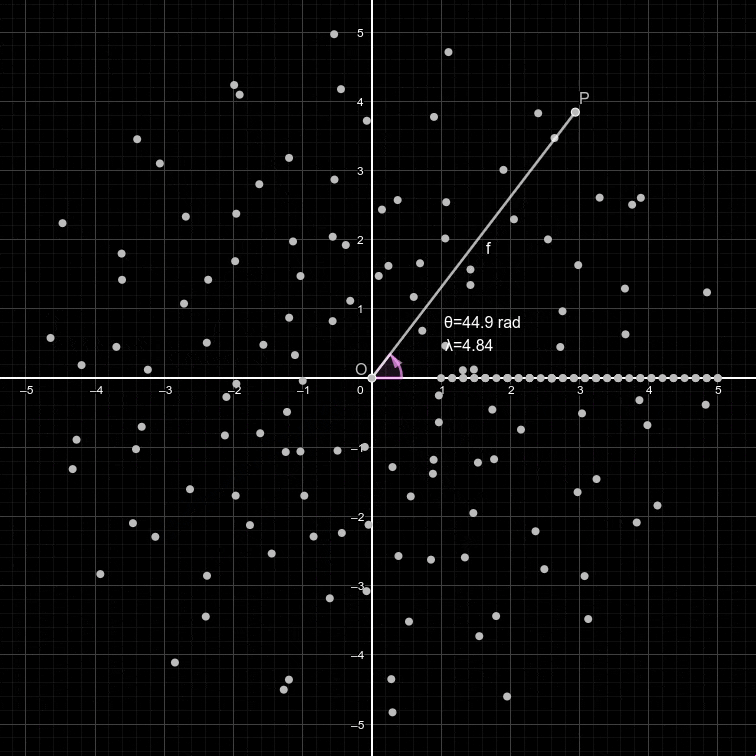
Ainsi, comme notre signal s'exprime en fonction du temps, exprimons l'angle $\theta$ selon le temps. De cette manière, lorsque notre signal augmente d'une unité, la rotation aussi. On a donc:
$\alpha \left[t\right]e^{i2\mathrm{\pi t}}$
Reprenons. Comme $2\mathrm{\pi }$ correspond à un tour autour du cercle, ici on a un avancement de t tours autour du cercle où t est le temps qui passe. Puisque nous voulons enrouler notre signal, qui lui aussi s'exprime en fonction du temps, autour du cercle, on écarte plus ou moins le point selon la valeur du signal au temps t (par multiplication, plus le signal est fort, plus le point sera loin de l'origine et vice-versa).
Cependant, comme on peut le voir sur l'animation plus haut les points semblent se positionner de manière assez désordonnée autour du cercle. Ainsi, afin de modifier la vitesse de rotation du point, on peut ajouter un paramètre dans notre forme exponentielle: la fréquence. On a donc:
$\alpha \left[t\right]e^{i2\mathrm{\pi ft}}$
Ainsi, en faisant varier f, on peut changer notre représentation enroulée d'un même signal:
Introduisons maintenant une nouvelle notion: celle de barycentre, ou de centroïde. Pour expliquer simplement ce principe, on peut imaginer notre signal comme un fil de fer: ainsi, dans cette représentation, il possède une masse. Et son barycentre serait alors son centre d'inertie, le point d'équilibre de la masse du fil. En mathématiques le centroïde est ainsi considéré comme le point correspond à la moyenne des points qui forment le signal/la forme considérée.
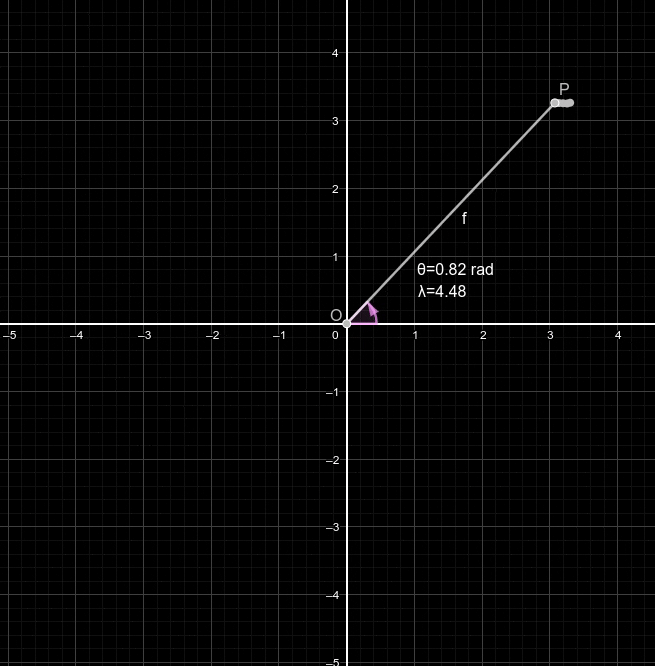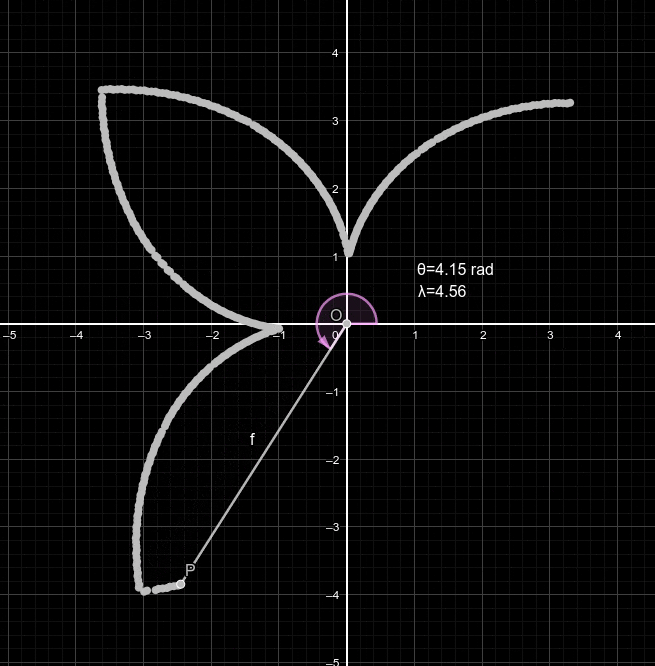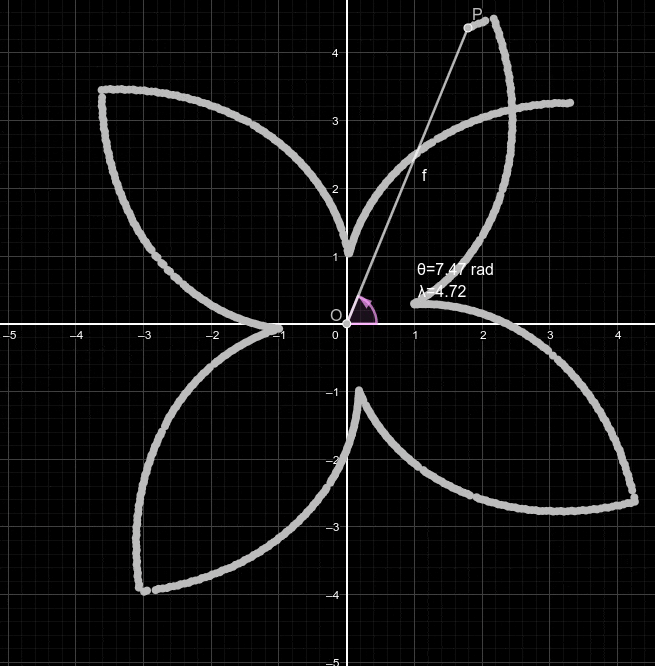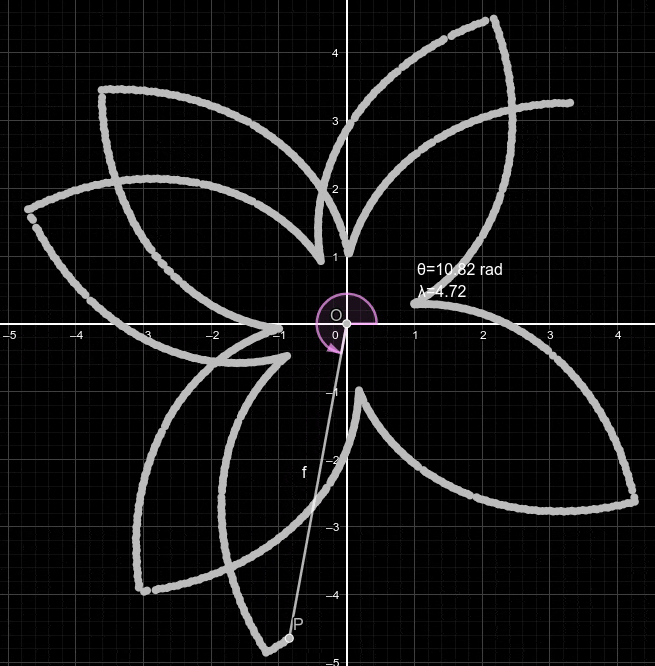
Ainsi, dans notre cas, en additionnant tous les nombres complexes de notrs ginal puis en diviant le résultat par le nombre total de points du signal, on obtient le barycentre. Voici une illustration montrant comment un centroïde (en rose) entre quatres points évolue suivant la position des points:
Retournons à notre enroulement de signal. Il nous est donc maintenant possible de calculer le centroïde de celui-ci grâce à une moyenne des n points qui forment la représentation enroulée du signal :
$\frac{1}{n}\sum _t^{n-1}\alpha \left[t\right]e^{2\mathrm{\pi ift}}$
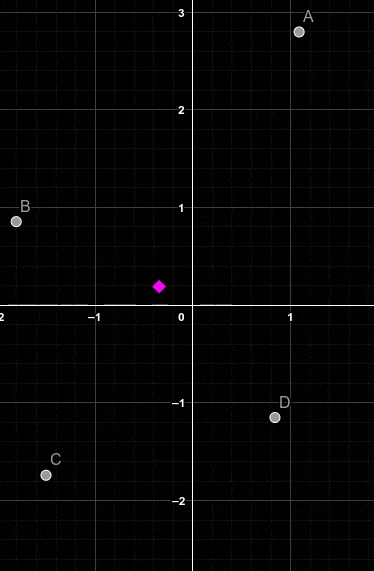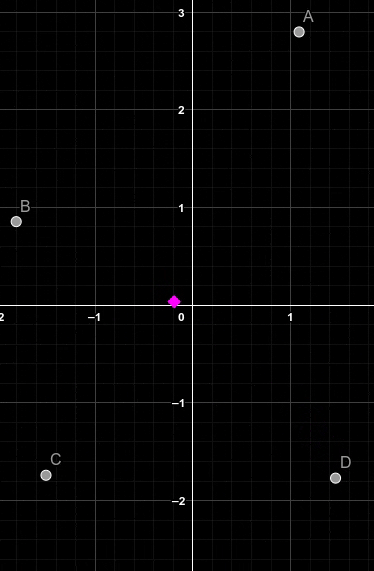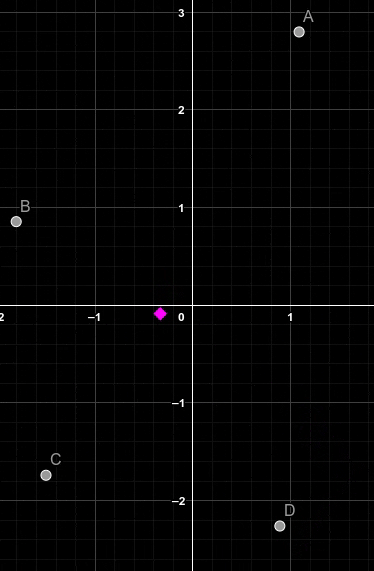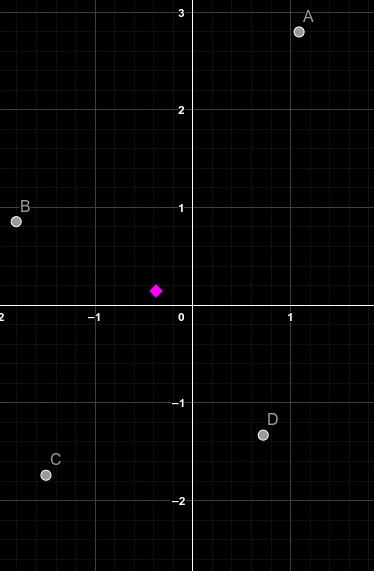
Si vous avez du mal avec la notation de somme cela revient à :
$\frac{1}{n}·\left(\alpha \left[0\right]e^{2\pi if·0}+\alpha \left[1\right]e^{2\pi if·1}+\alpha \left[2\right]e^{2\pi if·2}+\dots +\alpha \left[n-1\right]e^{2\pi if·\left(n-1\right)}\right)$
On peut donc créer une "fonction" $\sigma$ qui, suivant la fréquence f qu'on lui donne, nous donne le centroïde du signal à cette fréquence:
$\sigma \left[f\right]=\frac{1}{n}\sum _t^{n-1}\alpha \left[t\right]e^{2\pi ift}$
Et c'est à partir de maintenant que la magie de la transformation de Fourier peut opérer.
En effet, en temps normal, pour une fréquence f quelconque, le barycentre $\sigma$ es très proche de l'origine. En revanche, lorsque la fréquence f introduite dans $\sigma$ correspond à la fréquence originale du signal, le barycentre se retrouve anormalement éloigné de l'origine du repère.
On rappelle que le barycentre est un point représentant un seul nombre complexe. Ainsi, afin de calculer son éloignement par rapport à l'origine du repère, on peut calculer son module (dont nous avons déjà parlé). Ainsi, sur la courbe représentative du module du barycentre en fonction de la fréquence, les maximums globaux et locaux représentent les fréquences des sinusoïdes pures qui, une fois combinées, donnent notre signal.
Reprenons un tableau d'un signal:

Temps t (s)	1	2	3	4	5	6	7	8	9	10	11	12
Valeur	0	0.5	1	1.5	1	0.5	0	0.5	1	1.5	1	0.5

Maintenant calculons, à l'aide de $\sigma$, différents centroïdes et leur module de ce signal pour différentes fréquences:

Fréquence f	$\frac{1}{16}$	$\frac{1}{12}$	$\frac{1}{6}$	$\frac{1}{2}$	$1$	$1.5$
$\sigma \left[f\right]$	$-0.239+0.099i$	$-4.167·{10}^{-15}$	$-0.168-0.289i$	$0.083$	$0.75$	$0.083$
$\left|\sigma \left[f\right]\right|$	$0.259$	$-4.167·{10}^{-15}$	$0.333$	$0.083$	$0.75$	$0.083$

Ainsi, GAGARGAGAGARGAGAGARGARGAR les mathS JAJZJEJFJZNEl merde fourier = gros enculé HTML = grosse merde GNEUHGNEUH je retourne me coucher PK JSUIS UNE MERDE en fait c'est zidane qui rentre dans un bar